I'm Glad Sports Are Log-Normal
Normal sports would be too boring
Since we have no sports on this week, I figured I’d try and fill the gap with something “sports related”.
Background
I was recently reading some work by Allen Downey on the topic of normal vs. log-normal outcomes. Dr. Downey is the author of Think Python, Think Bayes, and he just recently came out with a new book called Probably Overthinking It, which is the inspiration for this post. He also just so happens to have a Substack if you’re interested in checking it out.
The basic premise of his idea around normal vs. log-normal outcomes is rooted in the central limit theorem and it’s various sub-theorems:
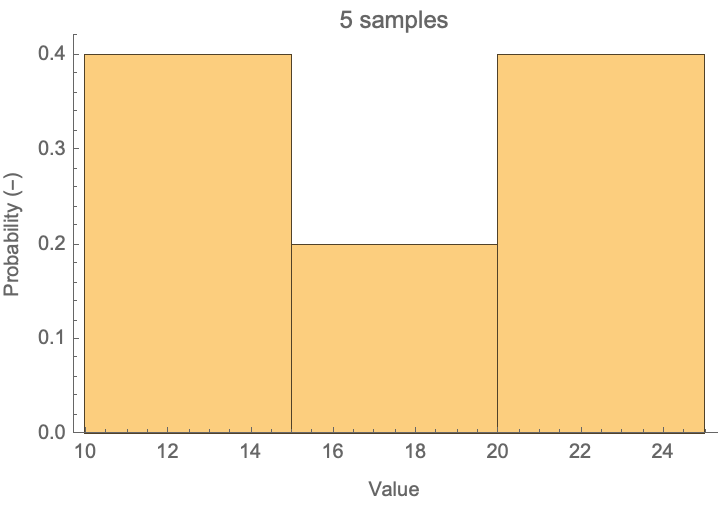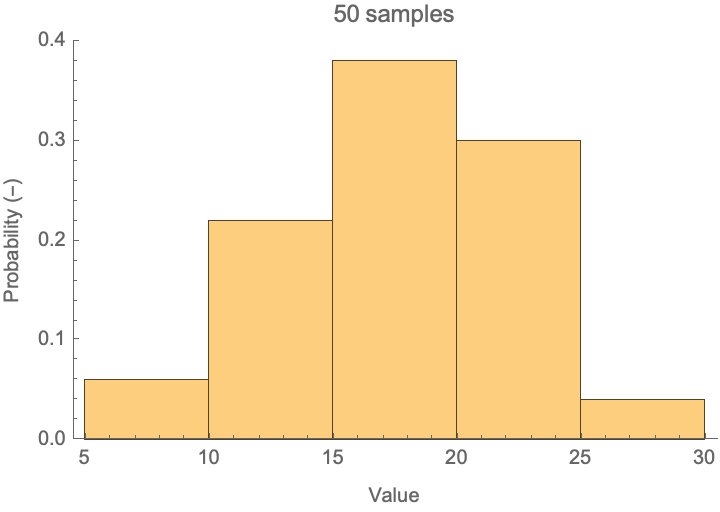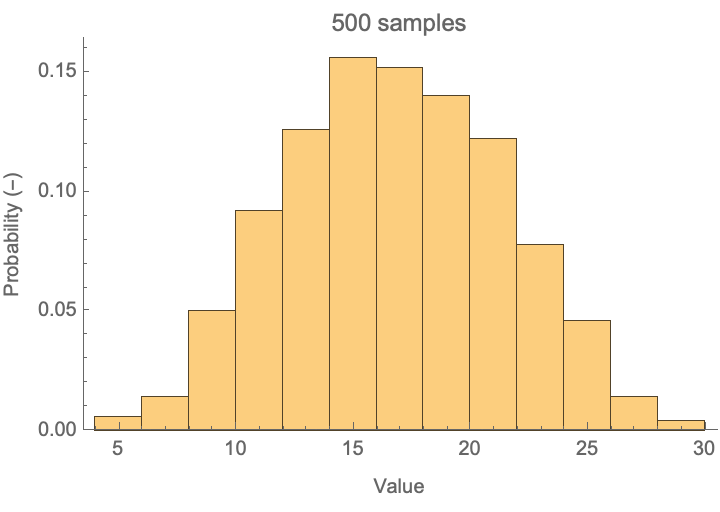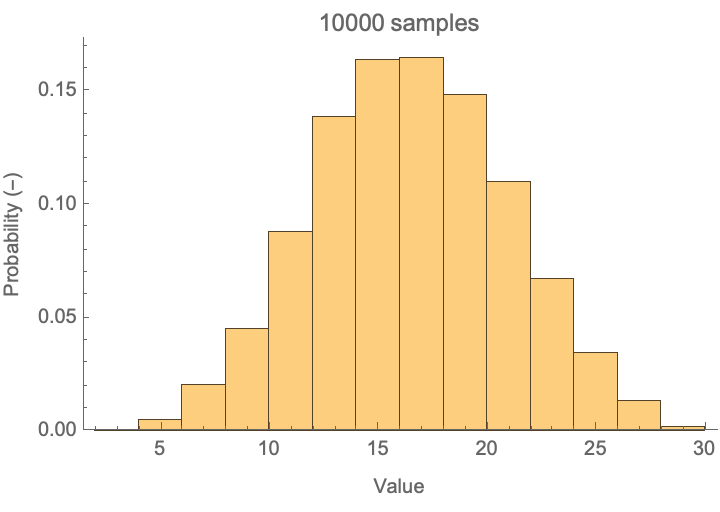
When you take effects that have stochastic components to them and combine them in an additive process, you will end up with a Gaussian, or normal distribution of possible outcomes. With enough samples, you will generate a nearly perfect bell shape as seen below.
However, when you take effects that have stochastic components to them and combine them in a multiplicative process, you will end up with a distribution of possible outcomes that is log-normal instead.
None of this is necessarily groundbreaking (although it’s neat to see), but the application of this to the world of sports is where things get interesting, and ultimately it's the reason we all like watching sports.
Normal vs. log-normal
Before talking about sports, let's understand what this theory is saying in a more practical sense.
To see this with an example, let’s look at the two main properties of a person’s physical characteristics, height and weight, from a dataset I obtained on Kaggle.
First up is a histogram of height (in cm) for ~8,000 people in this dataset. We clearly see a bell shaped curve consistent with a normal distribution. I don’t know the details of this particular sample of individuals, but we can see that the vast majority of heights fall in the range between 140 to 200 cm (4’7” to 6’7”), which feels reasonable. And more importantly, there appears to be equal representation to the left and right of the average somewhere around 166 cm (5’5”).
But what happens when we look at the weights of people? Shouldn’t that also be normally distributed? With a large enough sample of people, we should see people’s weight equally distributed on both sides of the average, right?
Well, not really. What we see instead is a bell shape curve that looks like its right side was “stretched” out. This is characteristic of a log-normal distribution. And what’s interesting is that you can see what is referred to as a ‘long-tail’ of possible values on that right part of the curve that stretch out quite far. They don’t happen frequently, but they can be quite extreme.
So, what is going on here?
The factors that contribute to a person’s height are mostly part of an additive process. Your height is made up of the lengths of the various key bones in your body starting with your legs and hips, and then torso, followed by neck and head. Most of this is determined by genetics, and outside of extreme surgery, can only be modified slightly by environment, nutrition, and other factors like that.
In contrast to height, a person's weight can be influenced by all of those same factors, but there is a multiplicative process underlying everything. Genetics, life style, environments, and any other contributing factors can compound on one another to produce more extreme behavior in weights than we see in heights.
The number of outliers and how extreme those outliers are is substantially larger in a log-normal distribution.
And yes, for those curious, as Dr. Downey points out, birth weights of babies ARE normally distributed. It’s only once the various effects have a chance to begin to play out and compound with one another, do we see the distribution shift to log-normal.
But how does all of this relate to sports?
Well, many of the important or exciting aspects in sports appear to favor log-normal behavior as opposed to normal. In fact, the distribution of sports abilities across the entire population is log-normal distributed.
To understand how this happens, it’s interesting to think through what it takes for someone to become a professional athlete. (And yes, there are lots of articles out there demonstrating the probabilities of your kid making it to the professionals that would indicate you’re better off as a parent focusing on their education instead of the world’s best sports training). You start first with the ‘gift’ of certain physical attributes and capabilities likely to allow one to excel in various sports. For a small number, those attributes are then compounded with childhood long practice and competition enabling them to go on to college sports. From there, select fewer will make it to the professionals. If you take an even smaller number of those with only the most extreme dedication, determination, and talent, you end up with hall of famer's. And finally, you sprinkle in a last little bit of intangibles, hard work, luck etc., you end up with the greatest of all time. This is the Wayne Gretzkys, Michael Jordans, and Tom Bradys.
The overall sports performance capabilities of people is log-normal. Dr. Downey said it best:
“Unless you are Usain Bolt, there is always someone faster than you, and not just a little bit faster; they are much faster.”
If sports abilities and performances were normal instead of log-normal, the difference between professional's and high-school glory day athletes would be pretty small. You’re average Joe could run against Usain Bolt at the Olympics and not be that far off.
Sports in a normal world would be…boring.
What about an example?
One of the first articles that ever went up on our Substack was an analysis I did looking at unexpected NBA performances along with my accompanying Python code. Recently, the NBA is in the news with people dropping ridiculous point totals in a game, so that article is suddenly very timely again (check it out below!).
A little over a week ago, Joel Embiid sent shocks through the league scoring 70 points for the Philadelphia 76ers. This was quite unexpected, but even more shocking, just a few days later it was followed up by Luka Doncic's 73 point performance for the Mavericks. In fact, thus far in the NBA season, there have been 5 games with an individual player scoring 60 or more points, the most in a season since 1962-63 season, which had 9.
However, despite how rare these performances seemingly are, they are completely possible in a log-normal sports world. Looking at the distribution of maximum points scored in a game for an individual player across the last ~70 seasons, we can see that the best player in a given game generally scores ~30 points. But there is a long tail of possible impressive performances consistent with a log-normal distribution. Scoring 40, 50, 60, and even Wilt Chamberlain’s 100 point performance in 1962 are possible in a log-normal sports world!
In a normally distributed sports world, the probability of seeing an NBA season with 5 60-pt performances would be << 1E-10. But, because we are lucky enough to live in a log-normal sports world, the chances of seeing the 5 performances we’ve seen so far in the NBA season is ~1.5%.
One more example
Just before the NCAA football championship, I looked at why a special teams coordinator should take the touchback on every kick off as opposed to trying to run it out. The analysis I did showed that by taking the touchback, you were much more likely to end up with better starting field position than if you tried to run it out.
Interestingly enough, however, there is evidence to suggest that kickoff returns may be log-normally distributed, with the caveat that you can’t run longer than the length of the field.
Without contradicting myself, the pseudo log-normal behavior on kickoff returns is the reason people think kickoffs are exciting. Just like watching an NBA game in Vegas, it probably wouldn’t be a good bet to place that someone is going to score 60+ points in a particular game and you also wouldn’t expect to see someone run a 100 yard kick off return in a game either. But 60 point games happen, and 100 yard kick off returns happen as well!
Wrapping up
Log-normal distributions have the same minimum that a normal distribution would have (0 in the case of many real-world things), but unlike the normal distribution, their upper limits can be MUCH higher. Ultimately, this means that the difference in abilities, points scored, home runs hit, etc. etc. can ALL be drastically larger than you would typically think and that’s what makes sports fun to watch.
As a fan of sports, I’d much rather watch log-normal performances.