Unexpected NBA Performances

An interesting approach to using statistics for sports analysis

Image from The Pudding

The early days of summer are always a good time of the year if you’re an NBA fan. The NBA has one of the longest post seasons of any professional sport and nearly every game is guaranteed to bring excitement with so much on the line.

Recently an interesting publication called the Pudding put out a video on YouTube discussing an analysis they conducted on the topic of unexpected performances in the NBA. Essentially, their goal was to determine the top unexpected performances in the NBA since the 1985 season. “Unexpected” is of course rather obscure, so they explained some of their criteria for determining it throughout the video. In this article, I’d like to walk through my attempt at reproducing that analysis.

Acquiring the data

The first step in this, and the one that the Pudding does not mention at all, is acquiring the data. We know that the metric used to assess unexpected performances involved player game scores. This is a metric developed within the NBA that factors in a number of other stats to try and determine how well a player’s performance was during a given game. To get data on player game scores, we’re going to need to collect these game score values for each player across every game they’ve played in their career.

A few quick searches for this information online fails to return any consolidated and reputable data sources. Fortunately for us, however, there is a nice Python package available, which calls into the stats.nba.com API’s to retrieve data in a very intuitive way. Let’s start first by loading some standard libraries as well as the NBA API package.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm

from nba_api.stats.endpoints import playercareerstats
from nba_api.stats.static import players
from nba_api.stats.endpoints import playergamelog

We’ll need a list of players that have played in the NBA in order to know who we should be retrieving records for.

allPlayers = players.get_players()
allPlayers = pd.DataFrame.from_dict(pd.json_normalize(allPlayers), orient='columns')

Once we have the player data, create a dictionary from the player ID to the player name.

nbaPlayerIDsToNames = dict(zip(allPlayers['id'], allPlayers['full_name']))

Now, for each player, their respective seasons, AND their respective games, let’s retrieve all the relevant stats available and create a single data frame from it.

NOTE: The following code takes a long time to execute (several hours)

Pauses have been added to the code to help prevent any timeout related errors with accessing the API’s.

nbaStats = pd.DataFrame([])
for playerID in allPlayerIDs:
    #print("Player ID")
    print(playerID)
    try:
        seasonIDs = playercareerstats.PlayerCareerStats(player_id=playerID, timeout=20).get_data_frames()[0]['SEASON_ID'].to_list()
        time.sleep(2)
        for seasonID in seasonIDs:
            #print("Season ID")
            #print(seasonID)
            nbaStats = pd.concat([nbaStats, playergamelog.PlayerGameLog(player_id=playerID, season=seasonID, timeout=20).get_data_frames()[0]])
            time.sleep(0.1)
    except:
        continue

Now that we have the data for all players and the games they played throughout their season, we need to calculate the game score for each game, which can be determined using the following formula:

Source: https://www.omnicalculator.com/sports/game-score

nbaStats["Game_Score"] = nbaStats.apply(lambda row: (row.PTS + 0.4*row.FGM - 0.7*row.FGA - 0.4*(row.FTA - row.FTM) + 0.7*row.OREB + 0.3*row.REB + row.STL + 0.7*row.AST + 0.7*row.BLK - 0.4*row.PF - row.TOV), axis = 1)

At this point, we should have very similar data to the analysis that the Pudding performed containing game score values for each player throughout their career. The last step is to clean up the data frame to reduce the size and keep only what we are interested in, which includes player names, game scores, and some information about game dates. We’ll also want to drop any Game_Score values which are not numeric (NaN’s).

nbaStats = nbaStats.drop(columns = ["Game_ID","SEASON_ID","MIN","FGM","FGA","FG_PCT","FG3M","FG3A","FG3_PCT","FTM","FTA","FT_PCT","OREB","DREB","REB","AST","STL","BLK","TOV","PF","PTS","PLUS_MINUS","VIDEO_AVAILABLE","WL"])

nbaStats["Full_Name"] = nbaStats.apply(lambda row: (nbaPlayerIDsToNames[row.Player_ID]), axis = 1)
nbaStats = nbaStats.dropna()

Analysis

Now that we have the data needed, we can begin the analysis. One of the first things we need to do is filter the players to only contain those that started their careers in the 1984-85 season or later (when the game score metric was officially created) in addition to those that played at least one season (82 games).

nbaStats["Game_Year"] = nbaStats.apply(lambda row: int(row.GAME_DATE[-4:]), axis = 1)

nbaStats = nbaStats.groupby("Full_Name").filter(lambda x: (x['Game_Year'] >= 1984).all())

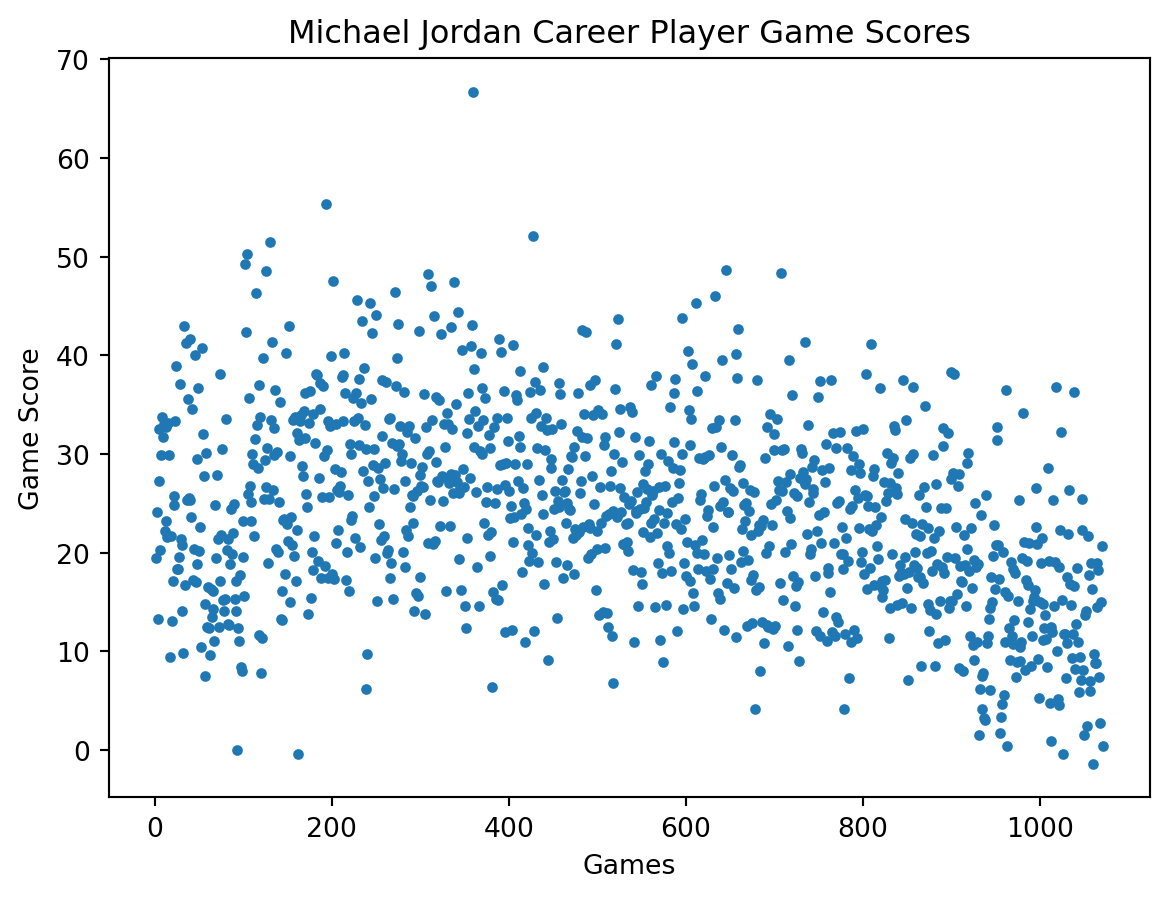
nbaStats = nbaStats.groupby("Full_Name").filter(lambda x: len(x) >= 82)

To make sure we’ve got things down correctly at this point, let’s see how Michael Jordan looked over his career. As mentioned in the Pudding video, Michael Jordan holds the record for the single best game score value ever at 64.6.

mj = nbaStats[nbaStats['Full_Name'] == 'Michael Jordan']

plt.plot(list(range(1, mj.shape[0]+1)), mj['Game_Score'], 'o', markersize = 3)
plt.xlabel('Games')
plt.ylabel('Game Score')
plt.title('Michael Jordan Career Player Game Scores')
plt.show()

In order to find “unexpected” games, we need to user a number of criteria. Unexpected can mean very different things for different players, which we want to capture. To do this, we’ll look at the z-score for each player’s game scores. Essentially this tells us how many standard deviations a particular game score is from the average value. Because the z-score is standardized, it gives us a chance to compare how rare a performance was for a player regardless of the actual game score. This is useful because not everyone is Michael Jordan, but that doesn’t mean they can’t have their own truly unexpected performances.

However, as was pointed out in the video, we still need some kind of criteria on the game scores. Otherwise we will end up with players who regularly scored 1 point, but had a single outstanding game of 10 pts. This will hit the mark on being unexpected, but doesn’t really qualify as a “great game”. To find that criteria, we can look at the distribution of game scores and find a value that marks the 99th percentile. That number happens to be ~29. As an interesting side note, if you go back and look at Jordan’s game scores, you’ll notice that he nearly averaged a game score value that is in the 99th percentile’s of all values for one portion of his career. Clearly very impressive.

percentile_99 = nbaStats['Game_Score'].quantile(0.99)

plt.hist(nbaStats['Game_Score'], bins=20)
plt.xlabel('Game Score')
plt.ylabel('Frequency')
plt.title('Histogram of Game Scores')

Using the great game criteria, let’s filter the data one more time for those players who had a least one great game in their career.

nbaStats = nbaStats.groupby("Full_Name").filter(lambda x: (x['Game_Score'] >= percentile_99).any())

Now we are setup to calculate game scores for each player across their entire careers. As mentioned above, doing this will help us to find truly unexpected performances as compared to how a player typically does.

nbaStats['ZScores'] = nbaStats.groupby("Full_Name")['Game_Score'].transform(lambda x: (x - x.mean()) / x.std())

The last thing we need to do is to sort based on the highest Z-Score values to determine the top 10 most unexpected performances.

top10UnexpectedPerformances = nbaStats.sort_values('ZScores', ascending = False).head(10)

top10UnexpectedPerformances.sort_values('ZScores', ascending = True).plot.barh(x = 'Full_Name', y = 'ZScores')
plt.xlabel('Z-Score')
plt.ylabel('')
plt.legend().remove()
plt.title('Top 10 Most Unexpected NBA Performances')

plt.show()

Based on this analysis, we agree with the Pudding’s findings that Willie Burton had the most unexpected NBA performance of all time. In that particular game, on December 13th, 1994 he scored 53 points while only averaging 7 points a game the entire previous season.

It’s worth noting that we have a few differences in the remaining top 10 as compared to the Pudding’s. It’s believed these are primarily the result of different data sources and to a lesser extent, one additional criteria that the Pudding included to look at the repeatability of unexpected performances.

Final thoughts

Related to overall top performances, it is of course easy to look at how many points players in the NBA score to determine how great they are. The game score metric provides a much broader perspective into performances because it captures many more key metrics. The G.O.A.T. debate is always a hot topic in the NBA, but I do find this plot showing the career game performances for Michael Jordan, Kobe Bryant, and LeBron James pretty interesting. I’ll leave it to the reader to infer anything they’d like from this, but obviously game score does not include the biggest metric of all - Championships.

def lowessFit(x, y):
    lowess = sm.nonparametric.lowess(y, x)
    lowess_x = list(zip(*lowess))[0]
    lowess_y = list(zip(*lowess))[1]
    return lowess_x, lowess_y

mj = nbaStats[nbaStats['Full_Name'] == 'Michael Jordan']
kb = nbaStats[nbaStats['Full_Name'] == 'Kobe Bryant']
lj = nbaStats[nbaStats['Full_Name'] == 'LeBron James']

mjX, mjY = lowessFit(list(range(1, mj.shape[0]+1)), mj['Game_Score'])
kbX, kbY = lowessFit(list(range(1, kb.shape[0]+1)), kb['Game_Score'])
ljX, ljY = lowessFit(list(range(1, lj.shape[0]+1)), lj['Game_Score'])

plt.plot(list(range(1, mj.shape[0]+1)), mj['Game_Score'], 'o', markersize = 1, color = "red")
plt.plot(mjX, mjY, color = "red")

plt.plot(list(range(1, kb.shape[0]+1)), kb['Game_Score'], 'o', markersize = 1, color = "purple")
plt.plot(kbX, kbY, color = "purple")

plt.plot(list(range(1, lj.shape[0]+1)), lj['Game_Score'], 'o', markersize = 1, color = "orange")
plt.plot(ljX, ljY, color = "black")

plt.xlabel('Games')
plt.ylabel('Game Score')
plt.title('Career Player Game Scores for\nMichael Jordan, Kobe Bryant, and LeBron James')
plt.legend(handles=[plt.gca().get_lines()[1], plt.gca().get_lines()[3], plt.gca().get_lines()[5]], labels=['Michael Jordan', 'Kobe Bryant', 'LeBron James'])
plt.show()