Empowering Your Own Healthcare
How To Read a Statistical Paper
Introduction
Many of us professionals in the oil and gas industry, despite our diverse disciplines, likely followed a similar trajectory in our younger years. We may have shown an inclination for math and science and were then nudged by parents, friends, and mentors to pursue a technical career in fields like engineering, chemistry, geology, or physics among others.
This also meant we likely followed a similar path in our math curriculums, starting with algebra, progressing to trigonometry, then advancing to various calculus courses (and if you're particularly unlucky, you might also have taken differential equations and linear algebra too…)
While these courses tend to be important in our day-to-day work, on our natural pathway to becoming a "professional nerd", many of us may have been pushed away from other math subjects, namely statistics.
We’ve written a number of articles around health on this Substack and with the rise in both access to information and AI, we see an important trend occurring where people are taking more steps toward understanding and looking after their own health.
Moving Mountains
The path to entrepreneurship is a strange one. Sometimes you hit bumps along the road. Sometimes roadblocks. And sometimes - without even stepping foot back in Colorado - sometimes you hit Mountains…
As part of that trend, one crucial skill is the ability to read and understand new findings in the field of health, which undoubtedly requires a basic understanding of statistics.
In this post, I wanted to walk through an example medical study, pointing out some of the key statistical concepts that are important to enable people to read these papers themselves and find meaning in the results.
Why Do We Need Statistics in the First Place?
Did you know that compared to calculus, statistics is actually quite young?
Most people have heard the infamous start of calculus when Isaac Newton was allegedly hit by a falling apple in the late 1600s. But while some initial theory development in statistics began in the 18th and 19th centuries, what we consider the field of statistics today really only emerged in the 20th century, several hundred years after calculus!
To me, it's fascinating that we developed theories for calculating planetary motion before understanding the practical applications of averages, hypothesis tests, and probabilities.
Before we dive into our sample article and explore the key considerations when reviewing statistics-based papers, it’s important to first understand why statistics is used in the analysis and presentation of results.
The goal of statistics is simple: to make informed decisions and draw reliable conclusions about a population using data from a sample.
In short, statistics help us quantify uncertainty, allowing us to make predictions, identify trends, and test hypotheses across various fields. At the smallest level, calculating the average of a set of numbers provides insight into the overall tendency of that group. On a larger scale, medical or health studies use statistics to examine a sample of people and infer what the findings might mean for the broader population.
Where is the Study From?
For this post, I’ll be referencing the article below from the New England Journal of Medicine. The article investigates cardiovascular safety of testosterone-replacement therapy in middle-aged and older men with hypogonadism (low testosterone).
https://www.nejm.org/doi/full/10.1056/NEJMoa2215025
Mentioning the source for this article brings me to my first point:
Make sure anything you are reading is from a reputable source, especially if you are looking at it as a source of medical information
The England Journal of Medicine falls into a category that’s broadly called peer-reviewed Journals and it happens to be one of the oldest and most influential medical journals in the world. Other reputable publishers in this category include:
The Lancet: A leading British medical journal that covers global health and clinical research, known for publishing landmark studies in medicine.
Journal of the American Medical Association (JAMA): JAMA publishes a wide variety of medical studies, including clinical trials, meta-analyses, and epidemiological research.
The BMJ (British Medical Journal): Known for its rigor, BMJ publishes original research, reviews, and evidence-based medicine studies.
Nature Medicine: A prominent journal focusing on the intersection of basic science and clinical research, covering areas like genetics, immunology, and drug development.
Annals of Internal Medicine: Published by the American College of Physicians, this journal focuses on internal medicine and clinical research.
Outside of peer-reviewed journals, other good sources of information can include government and international health agencies such as:
World Health Organization (WHO): Provides research and guidelines on global health issues, offering reports and studies based on data from various regions and countries.
National Institutes of Health (NIH): The primary U.S. government agency for biomedical and public health research. The NIH funds large-scale clinical trials and basic research.
Cochrane Library: A collection of high-quality systematic reviews that provide evidence-based analyses on a variety of healthcare interventions.
Finally, there are a growing list of other reputable sources which include:
PubMed/Medline: A free search engine run by the NIH that provides access to millions of abstracts and citations from a wide range of life science and biomedical journals.
Cochrane Collaboration: Known for its systematic reviews that synthesize clinical trial data, providing some of the most reliable evidence for healthcare decisions.
European Medicines Agency (EMA): A regulatory body that oversees the scientific evaluation of medicines in the European Union and publishes clinical data and reports.
U.S. Food and Drug Administration (FDA): In addition to regulatory functions, the FDA publishes clinical trial results and research on drug safety, medical devices, and public health.
How is the Study Setup?
Beyond who is publishing the study, the next most important piece of information to look for is how is the study setup?
In the case of our sample article, we see it mentioned right at the beginning that the study was multi-centered, randomized, double blind, placebo control and non-inferiority. That’s quite the mouthful, but here’s what each of these mean and more importantly why they are important:
Multi-center - The study was conducted over multiple locations or institutions, which means more people could be included and there was less bias introduced from the use of only one institution.
Randomized - Participants are randomly assigned to different groups (e.g., treatment or control). This helps reduce bias and ensure that any differences between groups are due to the treatment, not other factors.
Double blind - Neither the participants nor the researchers directly involved know who is receiving the treatment or placebo. This further reduces bias in the study.
Placebo control - One group receives a placebo (an inactive substance) instead of the treatment. This allows researchers to compare the effects of the treatment against no treatment.
Non-inferiority - The study aims to show that the new treatment is not worse than (or is at least as good as) an existing treatment by more than a pre-specified margin.
One of the most critical aspects to consider in studies is whether they are interventional or observational. In an interventional study, researchers actively test a specific variable (like a treatment or intervention) across different groups to determine its effects. We have all heard the phrase “correlation does not equal causation”. Well, when you setup a proper interventional study, it creates a scenario where correlation CAN be attributed to causation and that’s incredibly important.
In contrast to interventional studies, observational studies do not involve direct intervention by researchers. Instead, they observe and analyze existing groups or situations without manipulating variables. While observational studies can provide valuable insights, especially in situations where interventional studies may be impractical or unethical, they are generally considered less robust in establishing causal relationships due to the potential for confounding factors.
Our example article meets the gold standards for studies. It is interventional and it is setup from the beginning to try and ensure differences in outcome between various groups can be attributed to what is being tested and not an outside factor or bias of some kind.
What is the Null Hypothesis?
Once we have understood the study setup, the next important thing is to ensure we understand what exactly we are testing for and how the results should be interpreted.
In our example study, the high-level goal was to determine whether we see a difference in the number of adverse cardiac events between a group receiving testosterone-replacement therapy, as compared to a group that received a placebo.
However, how this is worded in studies is important because it defines what statisticians refer to as the null hypothesis:
The null hypothesis is a statement used in statistical hypothesis testing that proposes there is no effect or no difference in a population parameter, or that any observed effect is due to random chance. It serves as a default or baseline assumption, which researchers aim to test against the alternative hypothesis.
Typically the null hypothesis can be equated with the “status quo”. For example, if you are looking at whether there is something different between various groups, your null hypothesis would say by default that there is no difference.
This is obviously somewhat arbitrary however, and the authors may define the null hypothesis however they would like. So it’s important to interpret what they say correctly because the null hypothesis permeates to how the results are interpreted.
In the case of this specific study, it is mentioned to be a non-inferiority study, which is a common medical treatment type of study where we assume that there IS a difference between the groups and we assume the treatment is inferior. In the context of our study, it means our null hypothesis is that testosterone replacement therapy will have an inferior outcome to the placebo group in terms of cardiac events.
Statisticians make a big deal about the null hypothesis, but for the rest of us, it can most easily be thought of as our reference point for how to interpret the results.
What Are p-values?
Once we understand how the study was setup and what the null hypothesis is, we can generally begin to look at the findings including reviewing the statistical analysis. Before doing that, however, it is important to understand how exactly statistics makes its inference on the larger population based on a presumed sample of that population.
A key aspect of how this is possible comes from one of the fundamental theorems of statistics called the central limit theorem.
The central limit theorem (CLT) states that, given certain conditions, the arithmetic mean of a sufficiently large number of iterates of independent random variables, each with a well-defined (finite) expected value and finite variance, will be approximately normally distributed, regardless of the underlying distribution.
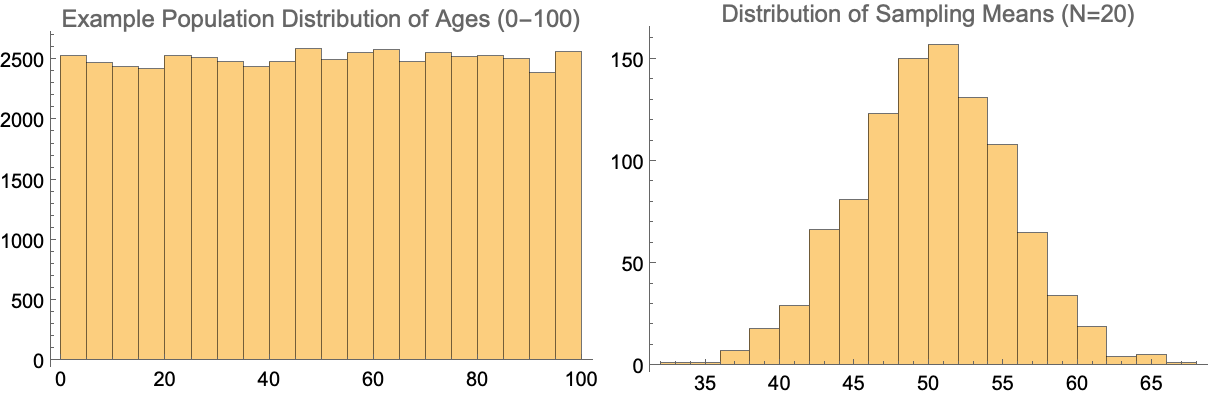
This is a fancy way of saying that despite what the distribution of a particular metric from the population looks like, if we were to continually pull a sample from it and take the average of that sample, we will end up with a normal distribution around the mean. And the reason statisticians like normal distributions so much is because they are easy to work with in terms of extracting probabilities and percentiles.
As a simple example, below we can see what happens if were were to look at an imaginary population with people having a uniform age between 0 and 100. If we then randomly sample that distribution (using 20 people each time in this case) and then take the average, that distribution of sampling means would be normal in its shape.
Now depending on what the study is looking at, there can be quite a bit of complexity in terms of how the statistical analysis is actually performed and I won’t go into those details in this post. But in each case, the end goal is to determine whether the results from comparisons across the various groups is what is referred to as “statistically significant”. And generally to reach this criteria means that the p-value returned from the hypothesis test was found to be less than or equal to 0.05.
The formal definition of the p-value is the following:
The p-value is the probability of observing a test statistic at least as extreme as the one actually observed, assuming that the null hypothesis is true.
What this means in simpler terms is that when analyzing the results of the study statistically, we assume our null hypothesis to be true and we then determine what the probability of seeing the outcome that we saw is under that assumption. Generally the 0.05 threshold comes from the idea that if we only see a 5% probability or less of the outcome occurring under the null hypothesis, then there is believed to be strong evidence that the null hypothesis is not true.
As a side note, the 0.05 p-value threshold may feel somewhat arbitrary, and it is. The value has been the long standing criteria for statistical significance, but there are growing factions of statisticians that believe in different thresholds or even a whole other perspective on interpreting the p-value. Despite this, in academic studies, this value is still the primary criteria for determining evidence against the null hypothesis and it can be the difference between receiving further funding or not.
Conclusions
That’s a wrap!
In the case of our example article, the null hypothesis is that the use of testosterone-replacement therapy is inferior in terms of leading to more cardiac events. The p-value from the study for non-inferiority was < 0.001, which means there was overwhelming evidence against the null hypothesis. This indicates a very strong likelihood that testosterone-replacement therapy has no effect on cardiac events, which is of course good for any patients that have utilized this in the past or may wish to utilize it in the future to treat low testosterone. As the article states itself:
In men with hypogonadism and preexisting or a high risk of cardiovascular disease, testosterone-replacement therapy was noninferior to placebo with respect to the incidence of major adverse cardiac events.
As far as what we covered about reading statistical based studies, here’s a quick recap:
Consider the source of the study, favoring reputable peer-reviewed journals and established health organizations.
Differentiate between interventional studies (which can establish causation) and observational studies (which mainly show correlation).
When reading statistical papers, focus on the study setup (e.g., randomized, double-blind, placebo-controlled) to assess the quality of the research.
Understand the null hypothesis, which serves as the baseline assumption for statistical testing.
Be aware of the central limit theorem and its importance in statistical inference.
Pay attention to p-values, which indicate the statistical significance of the results (typically using a threshold of 0.05).