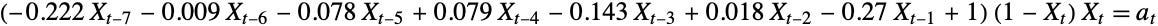Data Modeling: When Will We Reach 1,000 Followers?
Self-reflection on Pontem's followers through data science
In general, I’m not a fan of social media. I deleted Facebook and Instagram years ago and have somehow avoided getting thrown on the TikTok bandwagon.
However, I think LinkedIn is different. The focus is around keeping up with colleagues and clients in terms of their professional roles and it’s full of content I actually find interesting. Plus for most companies like Pontem, it’s a requirement to be at least somewhat active on LinkedIn.
But to make social media just a bit more interesting (to me, at least), what if I throw in a data science angle to it? Can we use data science to help us better predict Pontem’s follower growth? More specifically, let’s see if we can predict when Pontem will reach 1,000 followers on LinkedIn and maybe at the end of the year, we’ll revisit just how well our predictions played out.
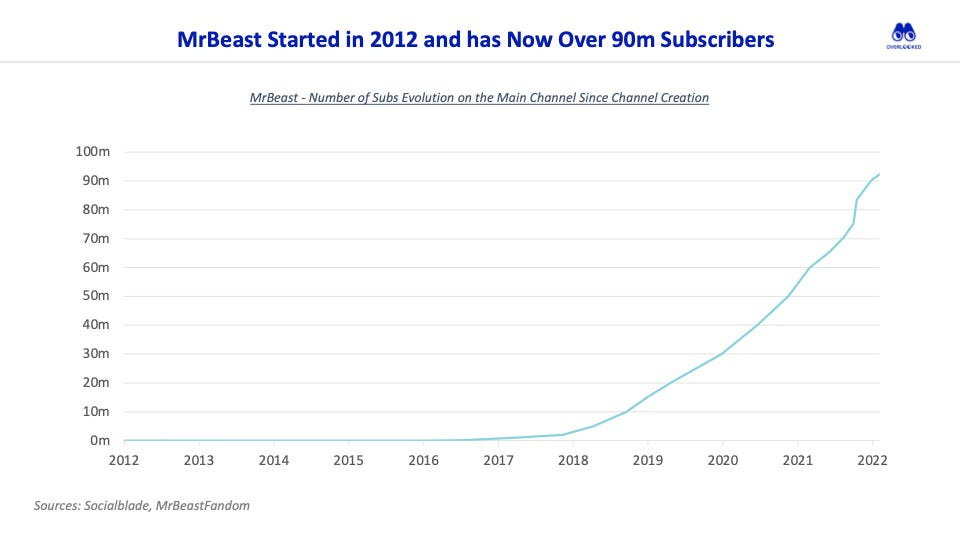
For background, here’s a snapshot of our follower growth since we started Pontem up until March-25. And yes, we are still pretty small, so our follower count is “humbling”… but hey, it is growing! Even the famous Mr. Beast’s follower count had to start somewhere.
Predicting Pontem’s Followers Using Traditional Methods
Before looking at anything too complicated, let’s first look at this using more “traditional” approaches. At some point or another, we’ve all probably taken some data, thrown it in Excel, and then fit a trend line through it. Then, to make that fit just a bit better, we’ve probably increased the polynomial degree (but hopefully stopped well short of a 20 degree polynomial that goes through every single point).
Well in this case, we appear fortunate enough to be on a relatively linear, if not ever so slightly exponential trajectory (one can hope). So let’s look at the fits of both such models and then we can see how they compare in terms of when we would be expected to reach 1,000 followers.
In the results above, our more sophisticated model (polynomial fit) looks to provide a very good match to the past follower count and also shows a rather optimistic perspective on what we could possibly expect from our future growth. In contrast, the linear model assumes we tend to increase in followers at a constant rate and therefore has a much more conservative perspective of our follower growth.
But can we do any better than this in terms of our predictions?? Potentially we can, but to do so we must enter the world of time series.
Introducing Time Series
Time series are fascinating and in my opinion, they rarely get the attention they deserve. To try and describe why time series are important as easily as I can, consider the following:
We are all relatively comfortable with the idea of two variables being correlated with each other. For example, someone’s height is typically correlated with their weight.
But what about when a single variable is correlated with itself, or more specifically, it is correlated with past values of itself?
When past values have a direct effect on future values, we enter the world of time series.
One of the most basic models of a time series is referred to as an auto-regressive time series. In the example below, we have an auto-regressive time series of order 1, meaning that current values are correlated, to some degree, with the immediate last value (and in this case in a positive and strong manner).
When a process is positively correlated with it’s past value, you can end up with a “wandering” behavior like we see above. In contrast, when a process is negatively correlated with it’s past value, you can instead end up with an oscillatory behavior as seen in the plot below, which is also an AR(1) with the same coefficient as the previous, but negative instead of positive.
Of course, this is just the tip of the iceberg on time series. A full breakdown on time series is well beyond the scope of this article. But to give you a flavor of where else they can go, here’s a collage further below of various (increasingly more complicated) random realizations from various time series models. The complexity here, can help us to understand why time series might be useful in so many applications (and we’re not even touching on multi-variate time series either).
The final example shown comes from what is called a SARIMA time series model, which stands for Seasonal (S) - Autoregressive (AR) - Integrated (I) - Moving Average (MA). Here is a breakdown of the top behaviors that can make up a time series:
Autoregressive (AR) - Captures the relationship between an observation and a specified number of lagged observations
Integrated (I) - Current values are additive with past values and thus if you difference them, you will make a time series more stationary
Moving average (MA) - Any error terms can be modeled as a linear combination of error terms occurring at the same time
Seasonal (S) - The time series tends to repeat at regular periods
But many models can contain only certain aspects of this. For example you can have AR, MA, ARIMA, SARMA, in addition to SARIMA models.
TL:DR: - time series practitioners really love abbreviations!
Predicting Pontem’s Followers Using Time Series
Getting back to our predictions, we clearly see evidence of a trend in the data (follower count is increasing), which would lead us to believe we have an integrated term in the model we need. If we were to difference our data, we would also see that our resulting time series appears stationary, meaning it’s properties do not depend on the time at which the series is observed nor does it have seasonal patterns.
After fitting our follower count to a time series model, we find that an ARIMA(7,1,0) returns the best fit. This confirms that we have a trend in our time series and that our values are also auto-regressive with up to 7 previous values (potentially there is more to explore there about how different followers accumulate throughout a week long period). Worth noting that in this case our MA term is 0, which is common as MA contributions tend to be small relative to AR.
Wrapping Up
So after all that, here’s a summary of when Pontem will hit 1,000 followers on LinkedIn for each of the 3 models we produced. The first two were more traditional approaches, while the last one is a time series based model. The confidence intervals here are plenty wide, so in reality these estimates likely overlap (get out of jail free card on our predictions!). But, since we’ll be keeping an eye on this and can come back to it, let’s take each one for their single prediction estimate.
We’ll check back in to see how these predictions are lining up. Who knows, maybe we’ll go viral by then.