Chutes and Ladders

A statistical approach

A timeless classic

Nearly everyone has probably heard of the game "Chutes and Ladders". You likely played it when you were a kid, or maybe you're like me and also play it with your kids now. It's a very simple game meant for young kids that involves zero strategy whatsoever, relying only on chance to determine who wins.

A few nights ago, I was playing with my four year old and having not played it since I was a kid, the game felt oddly long to me. I had no real basis to think that, but we had each spun our dial for what felt like around 30 times before seeing a winner and by intuition that felt “long”. So, naturally I was curious whether this was in fact a rare event or not. To try and answer that, I setup a simple simulation of the game to understand how many turns we would typically expect to reach a winner, which I will discuss below.

Analysis

As mentioned, the game is simple. There are 100 pieces on a board and at various locations there are "chutes", which are essentially slides, and then there are "ladders". If you land on a chute, you will slide back down to another predetermined spot. However, if you land on a ladder, you get to climb that ladder to some new location further along. Every one starts on the first spot and you spin a dial with values between 1 and 6 indicating how many steps you can take in your next move. The first person to reach the last piece at 100 wins.

Programming this is relatively simple in nearly any programming language. In this case, I'll be using the Wolfram Language.

First, you must create a way of describing the board. My approach to doing that, is to program in the location of each chute and ladder and the corresponding position you then move to should you land on one. Any piece you land on which is not a chute or ladder simply keeps you right where you are until the next time you spin.

(* Chutes *)
board[16] := 6;
board[48] := 26;
board[49] := 10;
board[56] := 53;
board[62] := 18;
board[64] := 60;
board[93] := 73;
board[95] := 75;
board[98] := 78;

(* Ladders *)
board[2] := 19;
board[4] := 14;
board[8] := 31;
board[21] := 42;
board[28] := 84;
board[36] := 44;
board[51] := 67;
board[71] := 91;
board[80] := 100;

(* Regular pieces *)
board[i_] := i;

Next, I'll create a single function that simulates the course of events in a game. Essentially, we use the board function defined above along with a random choice function (simulating the spinner) to help us move through the game. This is performed until the position 100 or greater is reached, which signifies that the game is done. I've placed an optional debug flag as an argument to the function that way I can perform some sense checks to make sure it is simulating the game as intended.

simulatePlayer[debug_:False]:=Module[{position,count=0,results},
	position=1;
	results=Reap[While[position<100,
		position=Sow[board[position+RandomChoice[Range[6]]]];
		count++
	]];
	If[debug,results[[2,1]],count]
]

simulatePlayer[True]
simulatePlayer[True]

With a quick look at the moves through a few sample games, everything appears to be working correctly. We can now move on to simulating a larger number of games, hoping to get an understanding of how long a single game can possibly take.

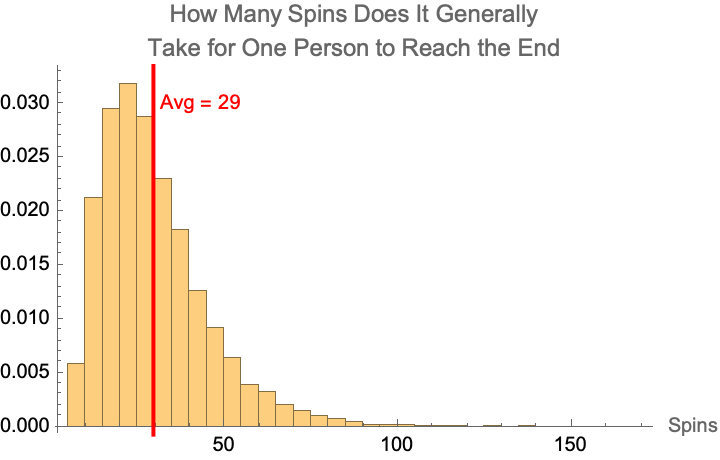
sims = Table[simulatePlayer[], 20000];

After examining the distribution of 20,000 games, we can see that it is skewed right. This intuitively makes sense. In theory, there is nothing stopping the game from going on indefinitely should you hit a span of (really) bad luck and continue to land on chutes that keep bringing you down. But of course, the likelihood of that occurring for really long spans drops quickly.

The main statistic we are interested in is the average number of spins it takes for a person to make it through the game, which was found to be ~29. So, as a first pass sense check, the game between my daughter and I may not have been particularly long after all. But we can’t stop with the analysis just there unfortunately.

The missing piece in the analysis above is that it shows how long it takes for ONE person to make their way through the board to win. Obviously, playing by yourself wouldn't be considered a very realistic scenario. So, to make the analysis more accurate, we need to understand how the expected number of spins per person changes as you add more players to the game.

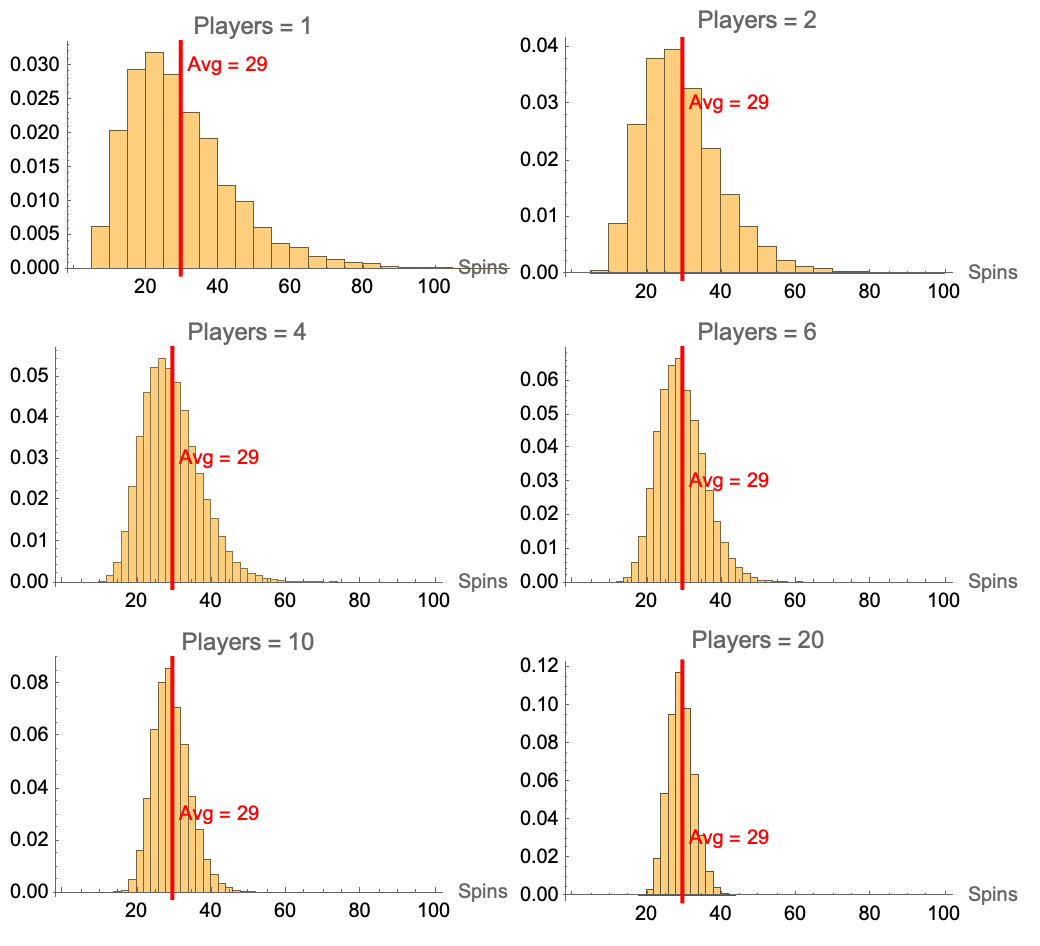
From the central limit theorem, we know that as more players play the game, the distribution of average possible spins per person to win will become more normally distributed around the average (instead of being right skewed). This means that as more people play the game, we would expect there to be less chances of any extremely long spin counts. This convergence actually happens relatively quickly as well. By having even just 4 players, we already start to show a more normal distribution. But we still aren’t quite done.

We also have to consider one more thing - because the game is over when the first person from a group wins, we are actually interested in what happens to the minimum spin count in a particular group, as opposed to the average. In this case, the central limit theorem will tell us that this too will become normally distributed as more players play, but we start to see that average spin count for the winner begin to decrease as opposed to converge on the average.

dist=FindDistribution[sims];
pdfOfSpinsWithPlayers = Table[
   	With[{pdf = 
      PDF[TransformedDistribution[Min[Array[x, players]], 
        Thread[Array[x, players] \[Distributed] dist]]]},
    		Table[{s, pdf[s]}, {s, 0, 100}]
    	],
   {players, 6}];

Or, shown another way, here is the average spins expected by the winner as the number of players increases. In theory, the spin count will continue to decrease but at a diminishing rate. The limit as the number of players continues to increase is 6, which is the fastest you can possibly win the game assuming you hit every single ladder.

Final thoughts

On average, my particular version of Chutes and Ladders will take someone playing by themselves about 29 spins in order to win. As more players get involved, the required number of spins from the winner is expected to decrease, potentially to somewhere around 12 spins in the case of 6 players.

So as it turns out, with just my daughter and I playing, each of us rolling for around 30 spins may have been slightly unusual as we would expect a winner after around 22 spins. But 30 is still a very plausible outcome. In fact, this would happen in roughly 17% of games.